Alice Game

题目大意

给定排成一排的n个怪物，每个回合，玩家可以选择两中操作之一：

  • 消灭一个大小小于或等于k的连续怪物序列，注意你必须消灭你选择的连续怪物序列中的所有怪物。
  • 消灭K个怪物，剩下的怪物按原序列分成两个非空序列。这两个序列将不被视为连续序列。

Alice先手，Bob后手，轮流操作，问Alice能否获胜。

解题思路

考虑SG函数打表找规律。

对于怪物数量x小于等于k时，直接转移到0，否则若怪物数量减去k大于等于2，即删去中间连续k个数后可以分成两个非空序列，枚举每个可以到达的状态，即枚举左右剩下的数量求sg值，当一个状态被分成两组时，这个状态的sg值为这两组状态的异或和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define int long long
#define x1 x111111
#define y1 y111111
#define x0 x00000
#define y0 y00000
typedef long long LL;
typedef pair<int,int> PII;
const double eps=1e-8;
bool multi=1;
int k,n;
const int N=1e6+10;
int f[N];

int sg(int x){
    if(f[x]!=-1) return f[x];

    unordered_set<int> S;
    for(int i=1;i<=k;i++){
        f[i]=1;
    }
    if(x-k>=2){
        for(int i=1;i<=x-k-1;i++){
            S.insert(sg(i)^sg(x-k-i));
        }
    }
    for(int i=0;;i++){
        if(!S.count(i)){
            return f[x]=i;
        }
    }
}

void solve(){
    for(int i=2;i<=100;i++){
        k=i;
        memset(f,-1,sizeof f);
        for(int j=0;j<=100;j++){
            if(!sg(j)){
                cout<<j<<' ';
            }
        }
        cout<<endl;
    }
}

signed main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int TTT=1;
    if(multi) cin>>TTT;
    while(TTT--){
        solve();
    }

    return 0;
}

程序中我们输出sg为0的情况，即先手必败情况。

0 3 13 23 33 43 53 63 73 83 93
0 4 18 32 46 60 74 88
0 5 23 41 59 77 95
0 6 28 50 72 94
0 7 33 59 85
0 8 38 68 98
0 9 43 77
0 10 48 86
0 11 53 95

取前面几组数可以看出规律，从上到下为k从2增大的情况，从左到右为n从0增大的情况。

易得当时，先手必败输出Bob，剩下输出Alice。

时间复杂度：O(1)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define int long long
#define x1 x111111
#define y1 y111111
#define x0 x00000
#define y0 y00000
typedef long long LL;
typedef pair<int,int> PII;
const double eps=1e-8;
bool multi=1;
int k,n;
const int N=1e6+10;
int f[N];

int sg(int x){
    if(f[x]!=-1) return f[x];

    unordered_set<int> S;
    for(int i=1;i<=k;i++){
        f[i]=1;
    }
    if(x-k>=2){
        for(int i=1;i<=x-k-1;i++){
            S.insert(sg(i)^sg(x-k-i));
        }
    }
    for(int i=0;;i++){
        if(!S.count(i)){
            return f[x]=i;
        }
    }
}

void solve(){
    // for(int i=2;i<=100;i++){
    //     k=i;
    //     memset(f,-1,sizeof f);
    //     for(int j=0;j<=100;j++){
    //         if(!sg(j)){
    //             cout<<j<<' ';
    //         }
    //     }
    //     cout<<endl;
    // }

    int n,k;
    cin>>k>>n;
    if(n%(4*k+2)==k+1){
        cout<<"Bob"<<endl;
    }else{
        cout<<"Alice"<<endl;
    }
}

signed main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int TTT=1;
    if(multi) cin>>TTT;
    while(TTT--){
        solve();
    }

    return 0;
}

Binary Number

题目大意

给定一个长度为的二进制数，你必须进行确定的次操作，每次操作选择一对数，翻转，输出k次操作后最大的二进制数。

解题思路

贪心，每次从左往右选择一段连续的变成。

但由于操作的是确定的k次操作，可能每一位全部变成了但不等于0。

记剩下的为

  • 当为偶数时，我们可以每次选择一个相同的区间，两次操作抵消，最终仍然全是。

当为奇数时，我们应该想办法进行一次操作使得原数不变而转化为偶数的情况。

  • k’为偶数
  • s中既有奇数又有偶数
  • s中有连续个0
  • s中有连续个1且k不为1

复杂度分析

时间复杂度：O(n)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<bits/stdc++.h>
using namespace std;
/*====================*/
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define int long long
#define x1 x111111
#define y1 y111111
#define x0 x00000
#define y0 y00000
/*====================*/
typedef long long ll;
typedef pair<int,int> pii;
/*====================*/
const double eps=1e-8;
/*====================*/
bool multi=1;

void solve(){
    int n,k;
    cin>>n>>k;
    string s;
    cin>>s;
    bool flag0=0,flag1=0;
    bool flag2=0,flag3=0;
    //flag0表示s中有0，flag1表示s中有1
    //flag2表示s中有连续个0,flag3表示s中有连续个1

    //先从左往右贪心
    for(int i=0;i<n;i++){
        if(s[i]=='0') flag0=1;
        if(s[i]=='1') flag1=1;
        if(s[i]=='1'&&i+1<n&&s[i+1]=='1') flag3=1;
        if(s[i]=='0'&&k){
            int j=i;
            while(j<n&&s[j]=='0'){
                s[j]='1';
                j++;
            }
            if(j>i+1) flag2=1;
            i=j-1;
            k--;
        }
    }
    //判断剩下的k'是否可以让原字符串不变
    //有四种情况：k'为偶数;s中既有奇数又有偶数;s中有连续个0;s中有连续个1且k不为1
    if(k%2==0||flag0&&flag1||flag2||flag3&&k>=3){
        cout<<s<<endl;
    }else{
        s[n-1]='0';
        cout<<s<<endl;
    }
}

signed main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int TTT=1;
    if(multi) cin>>TTT;
    while(TTT--){
        solve();
    }

    return 0;
}

Card Game

题目大意

规定一个牌堆按顺序递减放置时合法，现在给你一个数空位数n，需要你求出最大的数k使得初始状态在第一个空位按照从上到下放置，要求你在放置合法的前提下将其全部移动到其它同一个任意空位中。

解题思路

模拟找规律，记为n等于i时的答案，猜测，快速幂求解答案，提交顺利通过。

复杂度分析

时间复杂度:

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//a ^ b mod p
int qpow(int a,int b,int p){
    long long res=1%p;
    while(b){
        if(b&1) res=res*a%p;
        a=(long long)a*a%p;
        b>>=1;
    }
    return res;
}

void solve(){
    int n;
    cin>>n;
    cout<<qpow(2,n-1,mod)-1<<endl;
}

String Problem

题目大意

给定一个字符串，挑选个不相交的回文非空子段且子段最多有一个字符，求的最大值。

解题思路

观察到子段字符最多一个，所以每个子段只需考虑全为相同字符的情况。

显然，直接计算字符相同的最长连续子段贡献即可。

复杂度分析

时间复杂度：O(n)

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
/*====================*/
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define int long long
#define x1 x111111
#define y1 y111111
#define x0 x00000
#define y0 y00000
/*====================*/
typedef long long ll;
typedef pair<int,int> pii;
/*====================*/
const double eps=1e-8;
/*====================*/
bool multi=1;

void solve(){
    string s;
    cin>>s;
    int n=s.size();
    int res=0;
    for(int i=0;i<n;i++){
        int j=i+1;
        int cnt=1;
        while(j<n&&s[j]==s[j-1]){
            cnt++;
            j++;
        }
        i=j-1;
        res+=cnt-1;//连续字符长度减去这个连续字符组成的数量1
    }
    cout<<res<<endl;
}

signed main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int TTT=1;
    if(multi) cin>>TTT;
    while(TTT--){
        solve();
    }

    return 0;
}

foreverlasting and fried-chicken

题目大意

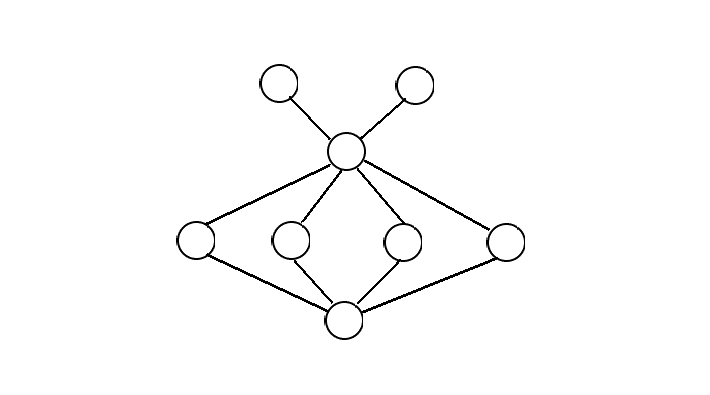
给定一个n个结点m条边的图，问这个图有多少个如图所示的子图。

img

解题思路

首先，这是我们要求得子图，如下图所示，我们每次计算1所在位置的贡献

image-20230720214340963

如下图，要求u的贡献，我们令u和v共同连向cnt个结点，u的度为ind[u]，那么u的贡献可表示为：

如上图所示，1向上连的那两条边不能包括4,5,6,7,8,所以ind[u]要减4，如果u还连向了v要再减1。

image-20230720214801583

用bitset存储边进行优化，判断两个点是否同时连向共同的结点，直接用bitset与操作，然后用count函数统计1的个数即为两点共同连向同个结点的数量cnt。

复杂度分析

时间复杂度：(w为计算机位数)

约不会超时

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<bits/stdc++.h>
using namespace std;
/*====================*/
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define int long long
#define x1 x111111
#define y1 y111111
#define x0 x00000
#define y0 y00000
/*====================*/
typedef long long ll;
typedef pair<int,int> pii;
/*====================*/
const double eps=1e-8;
const int mod=1000000007;
/*====================*/
bool multi=1;
// vector<vector<int>> edge;
int n,m;
const int N=1010;
int ind[N];
int c[N][N];




void solve(){

    cin>>n>>m;
    memset(ind,0,(n+1)*sizeof(int));
    bitset<1002> edge[1002];
    //bitset存储边
    for(int i=0;i<m;i++){
        int u,v;
        cin>>u>>v;
        ind[u]++,ind[v]++;
        //记录每个点的度
        edge[u][v]=1;
        edge[v][u]=1;
    }
    bitset<1002> tmp;
    int res=0;
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            tmp=edge[i]&edge[j];
            int cnt=tmp.count();//求出i,j两个结点共同连向点的数量
            if(cnt>=4&&(ind[i]-4-edge[i][j]>=2||ind[j]-4-edge[j][i]>=2)){
                res=(res+c[cnt][4]*(c[ind[i]-4-edge[i][j]][2]+c[ind[j]-4-edge[j][i]][2])%mod)%mod;
            }
        }
    }
    cout<<res<<endl;
}

signed main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    //杨辉三角预处理组合数
    for(int i=0;i<N;i++){
        for(int j=0;j<=i;j++){
            if(!j) c[i][j]=1;
            else c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
        }
    }
    int TTT=1;
    if(multi) cin>>TTT;
    while(TTT--){
        solve();
    }

    return 0;
}

SPY finding NPY

题目大意

给定一个数n，将形成一个随机全排列，你需要选择一个最小的k，使得最后获得的值最大的概率最大。

最后获得的数：对于任意排列，找到中最大的数，然后从向右找到第一个比前面找到的那个最大数大的数，如果没有则选择最后一个。

解题思路

显然我们要让找到最大的数即n。

当时，最大的数应该在第一个位置上，概率

当时，最大的数应该在上，令最大数位置为，则应该都小于的最大值。

第一个条件：最大数在上，对于每个，概率都为；

第二个条件：前面的最大值都位于，概率都为

（条件同时满足所以是相乘关系,而每种i的情况概率应该是相加）

总的概率

变形得到

而可以通过预处理的前缀和获得

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
#define endl '\n'

bool multi = 1;

const int N = 1e4 + 10;
double a[N];

void solve(){
    int n;
    cin >> n;
    double ans = 1.0 / n;
    int pos = 0;
    for(int k = 1; k <= n; k++){
        double d = (1.0 * k / n) * (a[n - 1] - a[k - 1]);
        if(d > ans){
            ans = d;
            pos = k;
        }
    }
    cout << pos << '\n';
}

signed main(){

    for(int i = 1; i < N; i++){
        a[i] = a[i - 1] + 1.0 / i;
    }

    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int T=1;
    if(multi) cin>>T;
    while(T--){
        solve();
    }

    return 0;
}